Lotka Volterra

Summer 2021 ~ @TitouanCh
Lotka Volterra equations are a system of differential equations used to model interactions between different species...

General Knowledge about Lotka Volterra

In the 1920's Alfred Lotka and Vito Volterra independently proposed the first mathematical model describing a predator-prey relationship.

This discovery would give birth new discipline: mathematical ecology or theorical ecology, the science of using mathematical, computational and conceptual models to study ecological systems like population dynamics or ecosystem interrelationships.

Above, you can see the predator-prey Lotka-Volterra model represented in a vector field. You can easily observe the cyclic nature of the model. It’s made by scattering random points on a graph, with the x coordinates and y coordinates representing the prey and predator population respectively. Then we can use our differential equations described below to draw a vector toward the next estimated position of our data point.

It's quite enjoyable to look at, have a go at changing the various parameters and see if you can make some abstract art. The graph’s colors evolve over time.

If the simulation is making your browser slow down, try lowering the number of points or pausing the Lotka Volterra simulation.

Two types of Lotka Volterra models

There are two types of Lotka-Volterra equations, let's take a look at the expression of their derivative

The Lotka Volterra predator prey model:


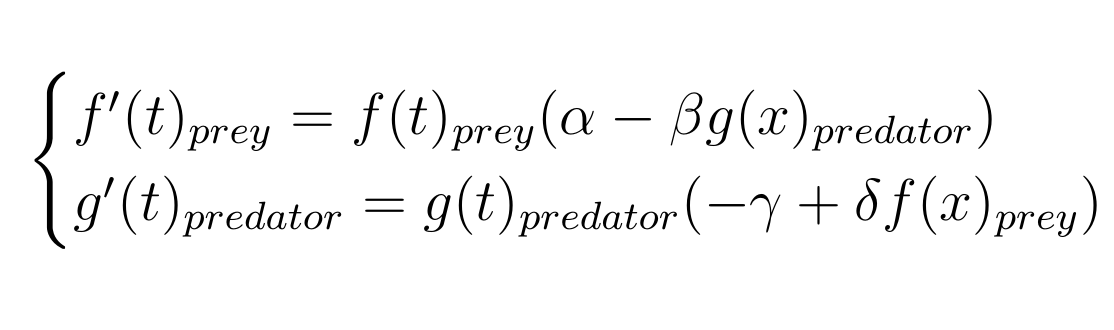Discovered first and the simpler version of the two, it's the model we chose to represent above in a vector field.

Frequently used to describe a system in which a predator and a prey interact. It can only simulate interactions between two species.

and the Lotka Volterra competition model:


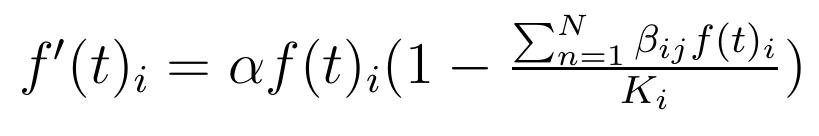Similar to the predator-prey model, this model takes into account any N species and can simulate more diverse interactions (predator-prey, mutualism, etc...).

The equation shown above is to compute the population of species i. Of course, it needs to be repeated as many times as there are species in our model.